برای اینکه نتیجه عملکرد سیستم فوق را بتوانیم بهتر درک کنیم از نموداری به این شرح استفاده میکنیم. ابتدا تابع  را رسم کرده و خط
را رسم کرده و خط 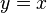 را نیز روی آن میکشیم. روی نمودار، مقداری اولیهای برای
را نیز روی آن میکشیم. روی نمودار، مقداری اولیهای برای  درنظر میگیریم. مقدار
درنظر میگیریم. مقدار  با رسم یک خط عمودی از این عدد تا نمودار
با رسم یک خط عمودی از این عدد تا نمودار  بدست میآید. برای بدست آوردن نقطه بعدی باید مقدار قبلی y را به جای مقدار فعلی x بگذاریم. این کار با رسم یک خط افقی از نقطه برخورد قبلی تا نمودار
بدست میآید. برای بدست آوردن نقطه بعدی باید مقدار قبلی y را به جای مقدار فعلی x بگذاریم. این کار با رسم یک خط افقی از نقطه برخورد قبلی تا نمودار 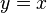 انجام میشود. شکلهای زیر با در نظر گرفتن
انجام میشود. شکلهای زیر با در نظر گرفتن 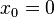 و به ترتیب، از راست به چپ،
و به ترتیب، از راست به چپ،  رسم شدهاند:
رسم شدهاند:





مشاهده میشود که با ایجاد تغییرات جزیی در پارامتر، رفتار سیستم کاملاً تغییر میکند. به چنین رفتاری «وابستگی حساس به شرایط اولیه» یا «اثر پروانهای» میگویند.
اگر مجموعه مقادیری که x در طول عملکرد سیستم به خود میگیرد را نسبت به c رسم کنیم، شکل بدست آمده یک فراکتال (برخال) خواهد بود:

تعریف ریاضی
یک بانقشه تکامل 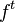 وابستگی حساس به شرایط اولیه دارد، اگر نقاط نزدیک به هم با افزایش t از هم جدا شوند. اگر M فضای حالت نقشه
وابستگی حساس به شرایط اولیه دارد، اگر نقاط نزدیک به هم با افزایش t از هم جدا شوند. اگر M فضای حالت نقشه 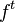 باشد، میگوییم
باشد، میگوییم 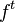 به شرایط اولیه وابستگی حساس نشان میدهد وقتی که حداقل یک δ>۰ وجود داشته باشد بطوری که به ازای هر نقطه x∈M و هر همسایگی از N که x را در بر داشته باشد، نقطهای مانند y در همسایگی N موجود بوده و در زمانی مانند τ رابطه
به شرایط اولیه وابستگی حساس نشان میدهد وقتی که حداقل یک δ>۰ وجود داشته باشد بطوری که به ازای هر نقطه x∈M و هر همسایگی از N که x را در بر داشته باشد، نقطهای مانند y در همسایگی N موجود بوده و در زمانی مانند τ رابطه  برقرار باشد.
برقرار باشد.
در این تعریف نیازی نیست که همه نقاط موجود در یک همسایگی، از نقطه مبنای x جدا باشند.
نظرات شما عزیزان: